Comparing Players

Throughout the history of basketball playstyles, coaching styles, and rule changes have drastically changed how the game is played. Comparing players in different seasons is difficult with all these factors taken into account. We can use how well a player compares to their season's average player in order to determine their effectiveness. We can use z-scores to do this. Learn about using z-scores to evaluate players here.

The 2-Sample Z-Test

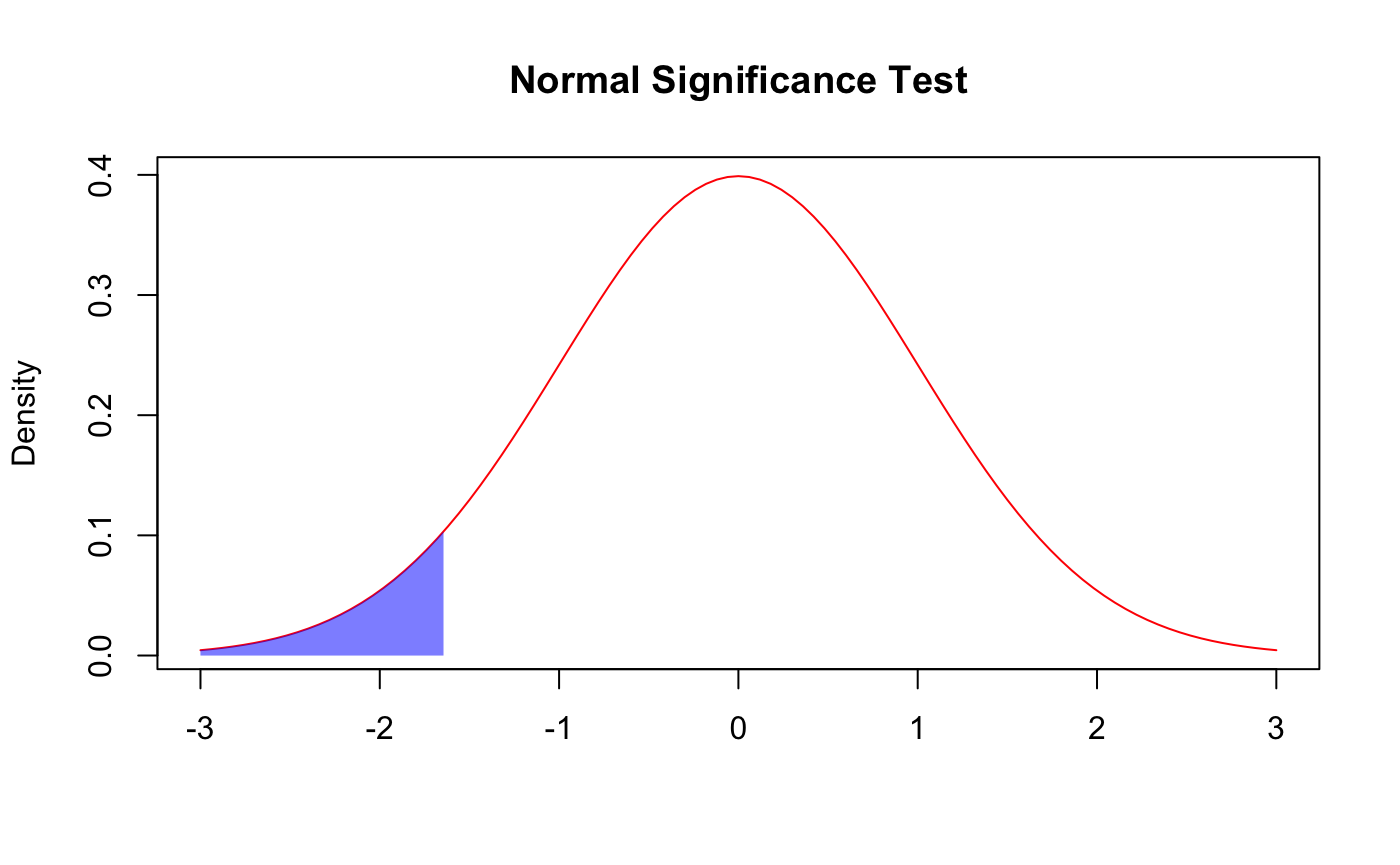
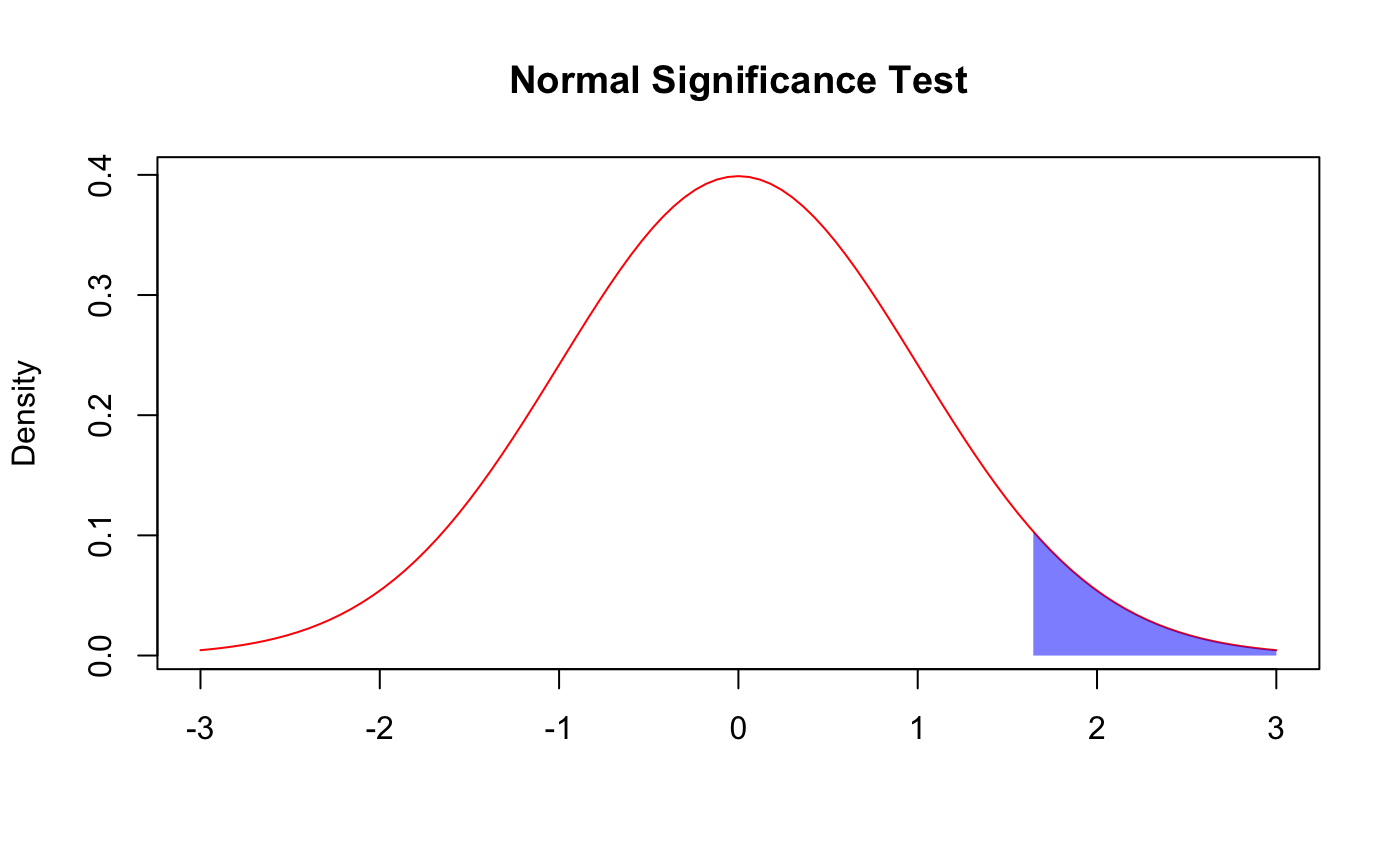
In order to compare 2 players we can do a significance test. We calculate the z-score of both players and do a significance test for each stat. We test the hypotheses: H0:z1 = z2 and H1:z1 < z2 where z1 is the z score of the player with a lower z score and z2 is the z score of the player with a higher z score. Z scores are normally distributed with a mean of 0 and a variance of 1. We can do a z-test with the formula: z=z2-z1/√((1/gp1)+(1/gp2)) where gp1 is the number of games played of player 1 and gp2 is the number of games played by player 2. When there are more games played we have more evidence that the players' averages are accurate to their true production. This is why the variance goes down when the games played is high. Then using the z-table we get the p-value of the test. If the p-value is less than 0.05 then we can conclude that player 2 is much better than player 1, if the p-value is above 0.05 but less than 0.10 then we can conclude that player 2 is slightly better than player 1, if the p-value is above 0.10 then we can conclude that player 1 and player 2 are about equal in this stat. We run this test for each stat that we are comparing in order to get a full comparision of the 2 players